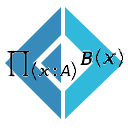Type All the Things

This article was posted as part of F# Advent 2018. Since originally publishing, release 0.4.0 adds SoomeDependentType for working with option types. See Tutorial for usage.

In computer science and logic, a dependent type is a type whose definition depends on a value. A "pair of integers" is a type. A "pair of integers where the second is greater than the first" is a dependent type...

This is a powerful idea that strongly-typed languages like F# can apply in the service of correctness. In this article I will

• introduce dependent types for F#
• discuss advantages in domain-driven design and development
• review performance benchmarks
• and finally, discuss how these are dependent types according to type theory

(Readers with strong opinions about dependently typed languages may want to read the final section first.)

Introducing Dependent Types in F#

There are several methods for creating ad hoc granular types, you may have used some of these.

DependentTypes are easy to instantiate and carry their semantic information with them.

We see from the tool tip data elements of this type are validated by a typed function in the PercentType module named PercentValidator, and that function has the signature unit -> float -> float option.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 

open DependentTypes

module PercentType =
    let validatePercent _ n = 
        match n >= 0. && n <= 1. with
        | true -> Some n
        | false -> None

    type PercentValidator() = 
        inherit Pi<unit, float, float option>((), validatePercent)

type Percent = DependentType<PercentType.PercentValidator, unit, float, float option>

printfn "%A" <| Percent.TryCreate 0.42
// Some (DependentType (Some 0.42))

By inheriting from the Pi type any total function may be used to construct dependent types. (Organizing the type and function in a module is a housekeeping convenience.)

Pi is a function that takes an element of a type to an element of another type. That is the essence of Dependent Types.

But why is unit necessary in the signature? Actually it is not an integral part of what the Pi function needs to be. unit in this case is a placeholder for a convenience feature. You can replace it with any type whatsoever to leverage the same function over similar DepenedentTypes.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 

module DigitsDef =
    let verifyDigits config value =
        regExStringVerify (new Regex("^[0-9]+$")) config value

    type DigitsValidator(config) = 
        inherit Pi<int, string, string option>(config, verifyDigits)

    type ValidDigits () = inherit DigitsValidator(0)
    type ValidDigits2 () = inherit DigitsValidator(2)
    type ValidDigits3 () = inherit DigitsValidator(3)
    type ValidDigits4 () = inherit DigitsValidator(4)

type Digits = DependentType<DigitsDef.ValidDigits, int, string, string option>
type Digits2 = DependentType<DigitsDef.ValidDigits2, int, string, string option>
type Digits3 = DependentType<DigitsDef.ValidDigits3, int, string, string option>
type Digits4 = DependentType<DigitsDef.ValidDigits4, int, string, string option>

printfn "%A" <| Digits.Create "093884765"
// DependentType (Some "093884765")

printfn "%A" <| Digits3.Create "007"
// DependentType (Some "007") 

printfn "%A" <| Digits3.TryCreate "0007"
// None

Notice this function reuse requires a second level of type inheritance.

If the Pi function results in an option, and you use TryCreate rather than Create to instantiate an element the resulting option is lifted ¹ to the resulting DependentType.

Dependent Typing All the Things

If it is important enough to validate data, why not type the validated data as we did above?

Option types are the mark of validated data. Some more examples available in the DomainLib include

• TrimNonEmptyString
• NonEmptySet
• integer in a range

But DependentTypes are for more than data validation. We are not restricted to emitting option types. Anything you can do with a total function you can type.

For instance ensure that DateTime is in UTC format.

1: 

type UtcDateTime = DependentType<UtcDateTimeDef.UtcDateTimeValidator, unit, DateTime, DateTime>

We can also categorize data with discriminated union types.

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 
18: 
19: 
20: 
21: 
22: 
23: 
24: 
25: 
26: 
27: 
28: 

type IntegerOfSign =
| PositiveInt of int
| Zero of int
| NegativeInt of int

module SumType =
    let intType _ (value : int) =
        match value with
        | v when v > 0 ->
            IntegerOfSign.PositiveInt v
        | v when v = 0 ->
            IntegerOfSign.Zero v
        | v ->
            IntegerOfSign.NegativeInt v

    type IntSumTypeDiscriminator() = 
        inherit Pi<unit, int, IntegerOfSign>((), intType)
    
type IntegerType = DependentType<SumType.IntSumTypeDiscriminator, unit, int, IntegerOfSign>

// DependentType (NegativeInt -21)
printfn "%A" <| IntegerType.Create -21

// DependentType (Zero 0)
printfn "%A" <| IntegerType.Create 0

// DependentType (PositiveInt 21)
printfn "%A" <| IntegerType.Create 21

DependentPairs

Another feature of Type Theory is the idea of Dependent Pairs. This is a typed pair of the original data element and the resulting dependently typed element. They are just as easy to create, relying on a Sigma type in place of the Pi type, and of course carry around their semantic information.

Future Directions

One thing DependentTypes cannot do, yet, is support extension members. Hopefully the implementation of these F# language suggestions will remedy this situation. ²

DependentTypes is still a work in progress. Please submit suggestions and feedback.

And my apologies to anyone who has suffered through a breaking change in the project. Hopefully we are at an end of those.

Benchmarking ³

Fine. But what about performance?

Let's benchmark...

DependentType option

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 

let runPctOption() =
    [|
        PercentType.validatePercent () 0.5
        PercentType.validatePercent () 2.5
    |] 

let runLiftedPctDependentType() =
    [|
        Percent.TryCreate 0.5
        Percent.TryCreate 2.5
    |] 

• Compare creating a percent DependentType option to creating a simple float option using the same validation logic.
• Each benchmark instance creates 1 Some option and 1 None option in both cases.
• Benchmark 1,000,000 instances, hence 2M option instances.

1: 
2: 

Validated option is faster than TryCreate DependentType option. 
f1 (21.9484 ± 2.5478 ms) is ~96% faster than f2 (607.0490 ± 15.8352 ms).

Not surprisingly validation and creation of a simple option is faster, 28X faster.

And it scales nearly linearly, as we see when executing the benchmark 10X instead of 1MX.

1: 
2: 

(10X) validated option is faster than TryCreate DependentType option. 
f1 (0.0006 ± 0.0000 ms) is ~94% faster than f2 (0.0091 ± 0.0002 ms).

Considering our DependentType option benchmark creates 2M option instances in less than 700 ms, and creates 20 in 9 micro-seconds, this is probably acceptable performance for all but the most demanding network applications.

The validation logic adds little overhead. Even comparing creating DependentType to "naked" options (not run through the validation logic) makes little difference in the performance ratio.

1: 
2: 

Naked option is faster than TryCreate DependentType option. 
f1 (18.3340 ± 0.1073 ms) is ~97% faster than f2 (601.7315 ± 4.2582 ms).

Can we squeeze even more performance from DependentType option creation? Let's use Create instead of TryCreate so we eliminate the overhead of "lifting" the 'T2 option result to the DependentType element.

1: 
2: 

Validated option is faster than Create DependentType. 
f1 (17.0064 ± 0.3517 ms) is ~93% faster than f2 (256.9292 ± 2.3419 ms).

Validate option is now only 15X faster, so the "lift" overhead of DependentType is noticeable at large scales (2M creations).

We expect from these results Create DependentType option is twice as fast as TryCreate, because it does not lift the option from the value to the DependentType. And we see if we do a Create to TryCreate direct comparison, that is roughly true.

1: 
2: 

Create DependentType is faster than TryCreate DependentType. 
f1 (258.6811 ± 1.3004 ms) is ~56% faster than f2 (592.7512 ± 2.1457 ms).

Consuming (reading) DependentType

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 

let readDependentType (xs : Percent option []) =
    xs
    |> Array.map ( fun x ->
        match x with
        | Some _ -> Some (someValue x)
        | None -> None )

let readVanillaOption (xs : float option[]) =
    xs
    |> Array.map ( fun x ->
        match x with
        | Some pct -> Some pct
        | None -> None )

1: 
2: 

Read Option is faster than Option DependentType. 
f1 (17.9776 ± 0.2142 ms) is ~33% faster than f2 (27.0092 ± 0.3793 ms).

• Reading 2M float options is only 33% faster than read/extract value operation on DependentTypes.

Substituting the verbose Some pct.Value.Value for the helper function someValue almost erases any advantage of float option.

1: 
2: 

Read Option is faster than Option DependentType Value.Value. 
f1 (19.5531 ± 0.1250 ms) is ~4% faster than f2 (20.2828 ± 0.1295 ms).

UtcDateTime DependentType

Benchmarking a type that is not an option, we compare UtcDateTime in the DomainLib to an implementation validating a DateTime.

This time 1M benchmark runs is also 1M instances.

1: 
2: 

Validated DateTime is faster than Create DependentType DateTime. 
f1 (278.7760 ± 3.3103 ms) is ~28% faster than f2 (385.8573 ± 0.6970 ms).

1: 
2: 

Read DateTime is faster than DependentType DateTime. 
f1 (7.3626 ± 0.0496 ms) is ~7% faster than f2 (7.9543 ± 0.0946 ms).

In this case the create and read performance differences are barely meaningful.

DependentPair

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 
14: 
15: 
16: 
17: 

module PercentType2 =
    type PairPercentValidator() = 
        inherit Sigma<unit, float, float option>((), PercentType.validatePercent)

type PercentPair = DependentPair<PercentType2.PairPercentValidator, unit, float, float option>

let runPctPair() =
    [|
        (0.5, PercentType.validatePercent () 0.5)
        (2.5, PercentType.validatePercent () 2.5)
    |] 

let runPctDependentPair() =
    [|
        PercentPair.Create 0.5
        PercentPair.Create 2.5
    |]  

Benchmarks comparing a validated option pair to DependentPair yields similar performance ratios to option DependentType.

1M runs again creates 2M instances.

1: 
2: 

Pair is faster than Create DependentPair. 
f1 (30.2823 ± 0.0807 ms) is ~86% faster than f2 (223.3536 ± 0.9640 ms).

1: 
2: 

Read pair is faster than DependentPair. 
f1 (28.5499 ± 0.0862 ms) is ~2% faster than f2 (29.0964 ± 0.1033 ms).

Creation of a simple validated tuple is 7X faster than creating a DependentPair, but read/consume performance is so similar we sometimes see the benchmark test failing because DependentPair performs faster.

But are these Dependent Types?

Yes, from the standpoint of Type Theory ⁴, no, if you believe Dependent Types can only exist in languages implementing formal proof architectures.

If F# were a so-called dependently typed language, this project would be called Refinement Types, because something called dependent types would already exist in the language, and rather than being defined by a Pi type function, dependent types would depend on inductive proofs. But F# is not now and never will be an inductively proven language. Try F* for that. ⁵

This is the maths notation for dependent types in type theory.

∏_(x:A) ^B(x)

It tells us that ∏ (Pi) is a function that takes an element of Type A and sends it to a family of Types, B. In other words, the resulting type (and its element value) depend on the input element value.

You see, Type Theory defines dependent types without regard to any proof. A dependent type is what it is by construction.

The F# type system does not allow for a family of types, but there are types that we can use to mimic a family of types.

• Any F# or .NET type, a family of one type.
• An F# option type, mimicking a family of two types.
• An F# discriminated union type, mimicking a family of arbitrarily many types.

Inductive proofs can support a powerful type system, but the difficulty in implementing and using such a language is attested to by the fact none of these languages have gone mainstream.

Correctness by construction is sufficient to achieve one simple thing we want from dependent types, granular type representation. And why name them something else when they so neatly fit in with theory? Non sunt multiplicanda entia sine necessitate. ⁶

Notes

¹ Lift usually has a different technical meaning within the context of functional programming. In this case the intuitive notion of lifting the option up a level seems right. What is “lifting” in Haskell?

² Not everyone has the skill and time to implement complex language features, but everyone can register their opinion as to which features are important to them.

³ The usual caveats about benchmarking apply. You should benchmark your own situation on your own system, etc. There is variance in running the benchmarks multiple times. The variance I saw was typically in absolute run time for each scenario, and not so much in the DependentType / control run time ratios. By and large these results are representative of typical benchmark runs on my system, FSharp.Core 4.5.3, net45 DependentTypes.dll

⁴ There are several different type theories. Most references in regard to programming and type systems mean some version of the lineage that began in the early 1970's with the work of Per Martin-Löf. For our purposes we refer to the Type Theory outlined in chapter 1 and appendix A of Homotopy Type Theory, Voevodsky, et al.

⁵ It is worth noting the definitive work on the preeminent dependently typed language, Software Foundations (Vols. I & II), barely mentions dependent types. Tracing the evolution of how proof assistant languages came to be called dependently typed would be an interesting article in its own right.

⁶ "Entities are not to be multiplied without necessity."

• DependentTypes
• Home page
• Benchmarks
• Type All the Things
• Get Library via NuGet
• Source Code on GitHub
• License
• Release Notes
• Getting started
• Tutorial
• Documentation
• API Reference